
Séance 4 :
Amélioration du filtre médian, définition des Staypoints, application des KMeans
8 Février
I. Présentation de la séance
A. Objectifs
Les objectifs pour cette séance sont multiples.
Dans un premier temps, nous avons souhaité améliorer la segmentation des trajectoires de la journée. En effet, les résultats obtenus par une simple approche sur la régularité des acquisitions ne sont pas assez précis. Un parcours peut être découpé en plusieurs segments et l'absence de mouvements (la personne reste chez elle pendant plusieurs heures) peut également se traduire par plusieurs segments. Nous pensons que ces erreurs sont inévitables tant que nous utilisons les délais d'acquisitions. Nous souhaitons implémenter une nouvelle approche fondée sur la détection de déplacements et de staypoints.
Dans la suite, nous souhaitons également nous pencher sur la reconnaissance des différents modes de transport au sein d'un même segment. Nous souhaitons pour l'instant reconnaitre 3 modes : rapide, moyen et lent. Le dernier correspondra à des déplacements à pied
Enfin, nous souhaitons améliorer notre filtrage médian, notamment en définissant un filtrage adaptatif.
II. Fonctions préliminaires
A. Imports
import gmplot
import parser
import filters
import distance
import colors
from projectColors import defineColorsList
import matplotlib.pyplot as plt
from tqdm import tqdm
from IPython.display import IFrame
lColors=defineColorsList()
B. Chargement des données
Chargement global¶
Nous avons choisi plusieurs journées "normales" du téléphone Androïd avec un nombre de points environ égal à 500 et durant laquelle l'utilisateur avait utilisé plusieurs modalités de transports. Ces journées sont :
- 14 décembre 2017
- 9 décembre 2017
- 5 décembre 2017
- 28 novembre 2017
- 25 novembre 2017
- 23 novembre 2017
android_df = parser.importJson("data/android_small.json", True)
android_df.head()
Chargement d'un jour particulier¶
day_df = parser.selectDate("14-12-2017", android_df)
gmap = gmplot.GoogleMapPlotter(45.764376, 4.810495, 13, apikey="AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM")
gmap.plot(day_df['latitude'],day_df['longitude'], 'cornflowerblue', edge_width=3)
gmap.draw("figure/4-day-df-wofilter.html")
IFrame('figure/4-day-df-wofilter.html', width=990, height=500)
II. Detection des Stay Points
Pour pouvoir détecter les modes de transports sur les trajectoires, il faut dans un premier temps détecter les phases "En mouvement" et les phases "Immobile".
Nous nous sommes donnés pour objectif de détecter les stay-point, c'est à dire les points pour lesquels l'utilisateur est immobile.
A. Détection de points d'intérêt
Objectif : on veut partitionner une journée donnée avec deux types de segments :
- segment "en mouvement"
- segment "immobile"
Algorithme #1¶
Notre première intuition était d'utiliser la vitesse pour cette segmentation, avec un règle du type
En mouvement : vitesse > threshold
Immobile : vitesse < threshholdCependant, cet algorithme donne de très mauvais résultats, car le bruit, même pour une trajectoitre filtrée est trop important. (Cf Notebook précédent avec le profil des vitesses)
Algorithme #2¶
Cette fois, on s'appuie sur la dentité des positions pour détecter le mouvement ou non.
L'idée est que si des points consécutifs sont suffisamment proche les uns des autres, l'utilisateur est à l'arret. La figure suivante illustre l'algorithme qu'on a imaginé :
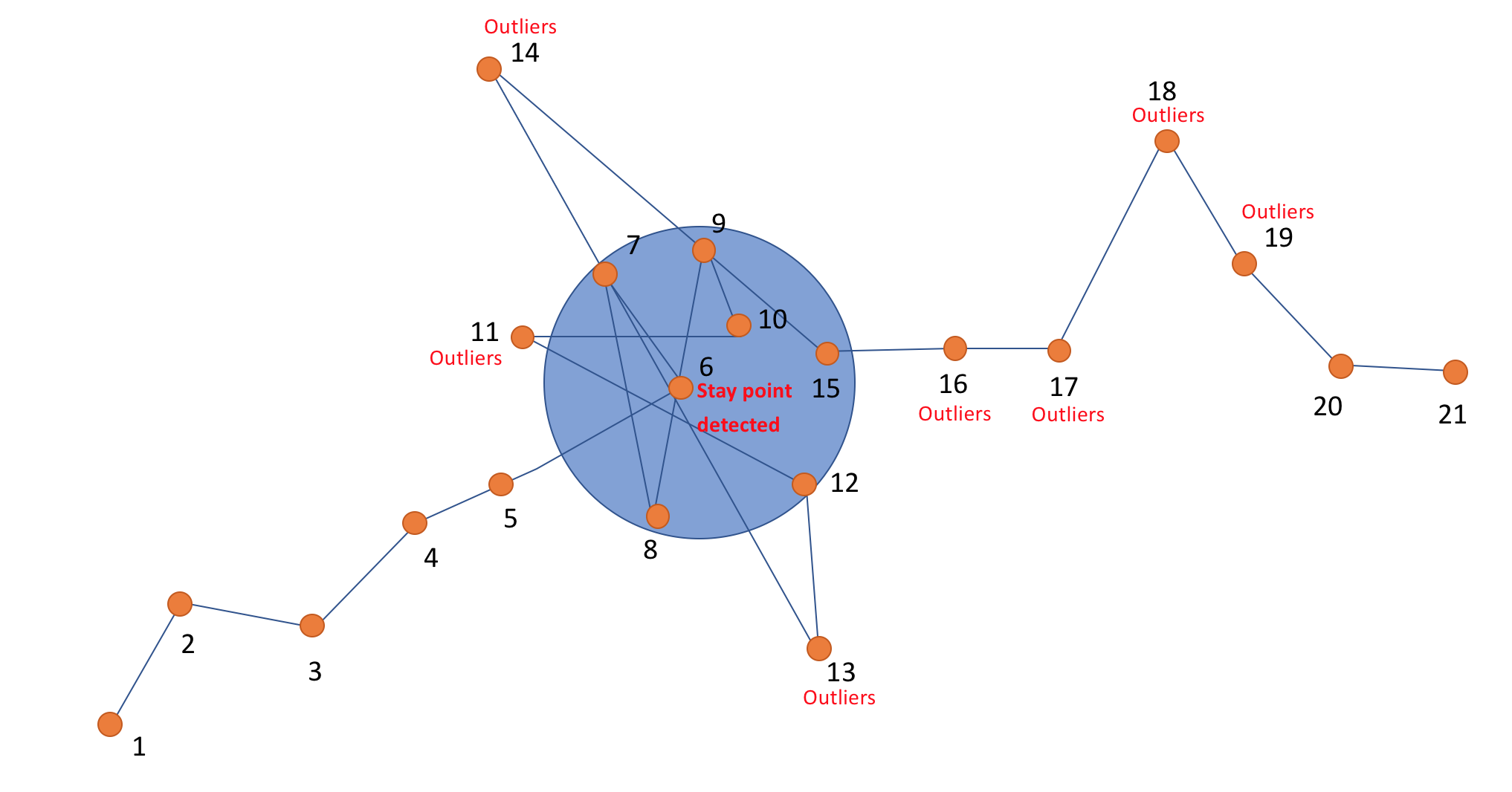
La Journée du 14 décembre, non filtrée et non segmentée :
On souhaite détecter que :
- Les points 1 à 5 sont en mouvement
- Les points 6 à 15 sont à l'arret, malgré le bruit
- Les points 16 à 21 sont en mouvement
Code de l'algorithme¶
Etape 1¶
Appliquer un mean filter sur la journée avec un fenêtre assez large, ici de 10 points. Cela permet de rapprocher les points "immobiles".
Remarque : une fois les Stay Points détéctés, on retournera sur les données non filtrées par le mean filter, car plus proche de la réalité.
day_df = filters.meanFilter(day_df, 10)
gmap = gmplot.GoogleMapPlotter(45.764376, 4.810495, 13, apikey="AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM")
gmap.plot(day_df['latitude'],day_df['longitude'], 'cornflowerblue', edge_width=4)
gmap.plot(day_df['lat_mean_filt'],day_df['lng_mean_filt'], 'red', edge_width=2)
gmap.draw("figure/4-day-df-med.html")
IFrame("figure/4-day-df-med.html", width=990, height=500)
Etape 2¶
Parcourir tous les points et détecter le début d'un Stay Point avec la règle :
Pour un point i donné, si les x points suivant sont à moins d'une distance radius de i, c'est un Stay Point.Dans l'exemple suivant, avec x = 4, le point 6 est le premier point du Stay Point.
# Distance between two filtered points
def fdistance(df, i, j) :
return distance.haversineDistance(
df["lng_mean_filt"][i],
df["lat_mean_filt"][i],
df["lng_mean_filt"][j],
df["lat_mean_filt"][j])
lower_limit = 3
radius = 50
i = 1790 # This is during a mouvement
start_stay_point = -1
while i < (day_df["timestampMs"].size - lower_limit - 1):
# Vérifier si i est un début de stay point
mouvement = False
for k in range(lower_limit) :
if (fdistance(day_df, i, i + k + 1) > radius) :
mouvement = True
if mouvement :
# Si on est en mouvement, regarder le point suivant
i += 1
else :
# Premier point immobile
start_stay_point = i
print("First Stay point : " + str(i));
break;
Etape 3¶
La 3eme étape est de détecter la fin du Stay Point.
On ajoute tous les points tant qu'ils sont à une distance inférieure à radius du point i.
On accepte jusqu'à k outliers de suite
Si k + 1 outliers sont détecté de suite, c'est la fin du Stay Point.Dans l'exemple, 11, 13 et 14 sont des outliers mais restent dans le Stay Point. A partir de 16, c'est de nouveau un segment "en mouvement".
max_outliers = 5
i = start_stay_point
outliers = max_outliers
j = i + 1
while outliers >= 0 and j < day_df["timestampMs"].size :
if fdistance(day_df, i, j) > radius :
outliers -= 1
else :
outliers = max_outliers
j += 1
i = j - max_outliers - 1
# Fin du stay_point
end_stay_point = i
print("End Stay point : " + str(i));
On ajoute tout ce code dans une librairie staypoint.py et on teste sur plusieur journées :
import staypoint as st
stay_point_df = st.findStayPoints(day_df, 3, 50, 5)
On affiche les trajets :
gmap = gmplot.GoogleMapPlotter(45.764376, 4.810495, 13, apikey=" AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM ")
segment_count = max(stay_point_df["segment_mouvement"])
for l in range(segment_count):
segment = stay_point_df[stay_point_df['segment_mouvement'] == l]
segment_mouvement = segment[segment['is_mouvement'] == True ]
gmap.plot(segment_mouvement["lat_mean_filt"], segment_mouvement["lng_mean_filt"], lColors[l%20], edge_width=4)
gmap.draw("figure/4-segmented-day-df.html")
IFrame('figure/4-segmented-day-df.html', width=990, height=500)
A l'inverse, on affiche les Stay Points :
gmap = gmplot.GoogleMapPlotter(45.783276, 4.771898, 14, apikey=" AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM ")
segment_count = max(stay_point_df["segment_mouvement"])
for l in range(segment_count):
segment = stay_point_df[stay_point_df['segment_mouvement'] == l]
segment_mouvement = segment[segment['is_mouvement'] == False ]
gmap.plot(segment_mouvement["lat_mean_filt"], segment_mouvement["lng_mean_filt"], lColors[l%20], edge_width=4)
gmap.draw("figure/4-stay-day-df.html")
IFrame('figure/4-stay-day-df.html', width=990, height=500)
Remarque : On pourrait agglomérer les Stay Points si ils sont trop proches les un des autres
On décide d'appliquer l'algorithme à d'autres journées, en faisant varier les paramètres et on obtient les résultats suivants :
Journée du 28 Novembre 2017¶
day_df1 = parser.selectDate("28-11-2017", android_df)
day_df1 = filters.meanFilter(day_df1, 5)
stay_point_df1 = st.findStayPoints(day_df1,3,20,5)
gmap = gmplot.GoogleMapPlotter(45.773593, 4.844522, 14, apikey=" AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM ")
segment_count = max(stay_point_df["segment_mouvement"])
for l in range(segment_count):
segment = stay_point_df1[stay_point_df1['segment_mouvement'] == l]
segment_mouvement = segment[segment['is_mouvement'] == True ]
gmap.plot(segment_mouvement["lat_mean_filt"], segment_mouvement["lng_mean_filt"], lColors[l%20], edge_width=4)
gmap.draw("figure/4-segmented-day-df1.html")
IFrame('figure/4-segmented-day-df1.html', width=990, height=500)
Journée du 25 novembre¶
day_df2 = parser.selectDate("25-11-2017", android_df)
day_df2 = filters.meanFilter(day_df2, 10)
stay_point_df2 = st.findStayPoints(day_df2,3,20,5)
gmap = gmplot.GoogleMapPlotter(45.790607, 4.835850, 12, apikey=" AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM ")
segment_count = max(stay_point_df["segment_mouvement"])
for l in range(segment_count):
segment = stay_point_df2[stay_point_df2['segment_mouvement'] == l]
segment_mouvement = segment[segment['is_mouvement'] == True ]
gmap.plot(segment_mouvement["lat_mean_filt"], segment_mouvement["lng_mean_filt"], lColors[l%20], edge_width=4)
gmap.draw("figure/4-segmented-day-df2.html")
IFrame('figure/4-segmented-day-df2.html', width=990, height=500)
gmap = gmplot.GoogleMapPlotter(45.757589, 4.831689, 14, apikey=" AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM ")
segment_count = max(stay_point_df["segment_mouvement"])
for l in range(segment_count):
segment = stay_point_df2[stay_point_df2['segment_mouvement'] == l]
segment_mouvement = segment[segment['is_mouvement'] == False ]
gmap.plot(segment_mouvement["lat_mean_filt"], segment_mouvement["lng_mean_filt"], lColors[l%20], edge_width=4)
gmap.draw("figure/4-stay-day-df2.html")
IFrame('figure/4-stay-day-df2.html', width=990, height=500)
On remarque donc que l'algorithme semble très bien fonctionner pour la détection de stay point. Il reste quelques améliorations à lui apporter, en effet on peut voir que :
- il faut agglomérer les stay-points qui sont très proches
- on ne recalcule pas le centre du cercle du stay point, et c'est pourquoi à Centrale on a plusieurs stay points. En effet si on se trouve à l'entrée de Centrale, les points à l'autre bout de Centrale seront considérés comme d'autres stay-points. Il faudrait donc recalculer le barycentre entre les points pour obtenir encore de meilleurs résultats
- le rayon pour la détection des stay-points est fixe, peut être que suivant les propriétes des points celui-ci devrait varier (le GPS fait plus ou moins d'écart)
- une condition sur le temps pourrait être ajoutée. En effet pour valider le fait que c'était bien effectivement un stay-point, l'utilisateur doit rester au stay-point au moins quelques minutes.
III. Classification des vitesses au sein d'un segment
Le but de cette section de classifier les différents régimes de vitesses au sein d'un segment de mouvement. Cette classification permet d'introduire une première identification des modes de transport :
- vitesse lente (marche à pied)
- vitesse moyenne (transports en commun ou voiture)
- vitesse élevée (voiture sur autoroute)
Cette classification s'opère en plusieurs étapes. Après avoir préparé les données, nous mènerons une classification en K-Means que nous deverons situer vis à vis de seuils de vitesse choisis par nos soins.
A. Préparation des données
Cette étape est consacrée au calcul de la vitesse et de l'accélération pour les points de la journée qui nous intéresse.
Nous définissons également une nouvelle colonne speedClass au sein du dataFrame pour porter l'information de la vitesse avec :
- -1: indéfini
- 0 : lent
- 1 : moyen
- 2 : rapidedef initSpeedClass(df) :
size = df['velocity'].size
accelerations = []
for i in range(size - 1):
accelerations.append(-1)
accelerations.append(-1)
return accelerations
day_df2['distance'] = distance.getDistances(day_df2)
day_df2['velocity'] = distance.getVelocities(day_df2)
day_df2['speedClass'] = initSpeedClass(day_df2)
day_df2.head()
B. Classification des vitesses
Nous pouvons visualiser le profil des vitesses de l'ensemble des segments.
plt.figure(figsize=(12,8))
plt.ylim(0,150)
plt.grid(True)
segment_count = max(stay_point_df2["segment_mouvement"])
for l in range(segment_count):
segment = stay_point_df2[stay_point_df2['segment_mouvement'] == l]
segment_mouvement = segment[segment['is_mouvement'] == True ]
plt.plot(segment_mouvement['velocity'], color=lColors[l%20])
Dans un premier temps, nous choisissons de travailler sur le segment 'vert pomme'; soit le segment compris grosssièrement entre 400 et 460 échantillons.
Ce dernier est suffisament long et comporte plusieurs régimes de vitesses.
Application à un segment particulier¶
Lorsque nous nous concentrons sur ce segment, nous obtenons le profil des vitesses suivant.
segNum=0
segment = stay_point_df2[stay_point_df2['segment_mouvement'] == segNum]
segment_mouvement = segment[segment['is_mouvement'] == True ]
plt.figure(figsize=(12,8))
plt.grid(True)
plt.plot(segment_mouvement['velocity'])
plt.show()
L'ensemble des fonctions consacrées à la classification des vitesses est contenu dans le fichier python speedClass.py.
import speedClassification as speedClass
Dans un premier temps, nous choisissons un nombre fixe de régimes de vitesses différents nbSpeedClass au sein d'un segment.
Pour l'instant ce nombre est fixé à 5.
(lK,whitened)=speedClass.applyKMeans(segment_mouvement,k=5)
lBoundiaries=speedClass.getBoundiaries(lK)
lFirstSpeedSegmentation=speedClass.calcFirstSegmentation(lBoundiaries,whitened,bPadd=True)
plt.figure(figsize=(12,8))
plt.grid(True)
plt.ylim(0,7)
for ii, plots in enumerate(lFirstSpeedSegmentation):
plt.plot(plots,lColors[ii%20])
plt.show()
Ci-dessus, nous avons donc la division de ce segment de mouvement en 5 sous-segments de vitesse homogène.
Il ne reste plus qu'à aggréger les segments qui ont une vitesse semblable.
(l,a)=speedClass.agglomerateSpeedSegments(lFirstSpeedSegmentation, lowThreshold=0.4, highThreshold=1.4,bMedian=False)
colorListSpeed=[
'seagreen',
'gold',
'tomato'
]
plt.figure(figsize=(12,8))
plt.grid(True)
plt.ylim(0,10)
for ii, plots in enumerate(l):
plt.plot(plots,colorListSpeed[a[ii]])
plt.show()
Ci-dessus, le graphique représente les sous-segments homogènes précédents classifiés par vitesse avec le code couleur suivant :
- vert : vitesse réduite
- orange : vitesse moyenne
- rouge : vitesse rapideApplication à l'ensemble des segments¶
Nous pouvons maintenant appliquer cette classification à l'ensemble des segments.
stay_point_df2.head()
stay_point_df2['speedClass']=initSpeedClass(stay_point_df2)
stay_point_df2['numSC']=initSpeedClass(stay_point_df2)
segment_count = max(stay_point_df2["segment_mouvement"])
for iSeg in tqdm(range(segment_count)):
segment = stay_point_df2[stay_point_df2['segment_mouvement'] == iSeg]
segment_mouvement = segment[segment['is_mouvement'] == True ]
if len(segment_mouvement['velocity'])>5:
(lK,whitened)=speedClass.applyKMeans(segment_mouvement,k=5)
lBoundiaries=speedClass.getBoundiaries(lK)
lFirstSpeedSegmentation=speedClass.calcFirstSegmentation(lBoundiaries,whitened,bPadd=False)
(speedAgglomerates,a)=speedClass.agglomerateSpeedSegments(lFirstSpeedSegmentation, lowThreshold=0.4, highThreshold=1.4,bMedian=False)
offset=0
for ii, plots in enumerate(speedAgglomerates):
for jj, speed in enumerate(plots):
stay_point_df2['speedClass'][segment_mouvement.index.tolist()[jj+offset]]=a[ii]
stay_point_df2['numSC'][segment_mouvement.index.tolist()[jj+offset]]=ii
offset+=jj
plt.figure(figsize=(12,8))
plt.subplot(211)
plt.plot( stay_point_df2['speedClass'])
plt.ylim(0,3)
plt.subplot(212)
plt.ylim(0,150)
segment_count = max(stay_point_df2["segment_mouvement"])
for l in range(segment_count):
segment = stay_point_df2[stay_point_df2['segment_mouvement'] == l]
segment_mouvement = segment[segment['is_mouvement'] == True ]
plt.plot(segment_mouvement['velocity'], color=lColors[l%20])
Le graphique ci-contre présente donc les profils de vitesses des différents segments, tels que nous les reconnaissons en haut et tels que nous les avons reçu en bas.
gmap = gmplot.GoogleMapPlotter(45.790607, 4.835850, 12, apikey=" AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM ")
segment_count = max(stay_point_df["segment_mouvement"])
for l in range(segment_count):
segment = stay_point_df2[stay_point_df2['segment_mouvement'] == l]
segment_mouvement = segment[segment['is_mouvement'] == True ]
for ispeed in range(3):
speedSegment=segment_mouvement[segment_mouvement.speedClass==ispeed]
gmap.plot(segment_mouvement["latitude"], segment_mouvement["longitude"], 'navy', edge_width=1)
for ii in range (5):
minidf=speedSegment[speedSegment.numSC==ii]
gmap.plot(minidf["latitude"], minidf["longitude"], colorListSpeed[ispeed], edge_width=3)
gmap.draw("figure/4-segmented-day-df2-bis.html")
IFrame('figure/4-segmented-day-df2-bis.html', width=990, height=500)
Nous pouvons alors reprojeter les différents régimes de vitesse sur les trajets dans Lyon.
On constate plusieurs problèmes :
- la présence d'effets de bords lors de la projection sur la carte
- des régimes de vitesse pas toujours cohérents
- dse segments de déplacement trop courts (seulement une dizaine de points)
IV. Filtrage par segment temporel
Les filtres mean filter et median filter utilisés jusqu'à présent s'appliquaient à l'ensemble des points. Or le relevé des points par le GPS peut s'arrêter pendant un temps suffisamment long pour que des points successifs n'aient pas de rapport direct entre eux, et donc ne devraient pas s'influencer lors du filtrage. Par exemple si l'utilisateur éteind son GPS pendant une heure, il n'est pas raisonable d'utiliser les points juste avant l'arrêt et juste après la reprise comme s'il s'agissait d'un même trajet continu.
Pour pallier à ce problème, on va utiliser l'algorithme de segmentation par seuil de délai entre deux points successifs présenté dans le notebook 2-segmentation. Cette fois on utilise un seuill plus grand de 400 secondes. Ce choix est motivé par l'observation des délais sur plusieurs échantillons où il semble que lorsque les cas dépassant les 400 secondes sont plus isolés et donc plus discriminant de différentes sessions d'activité.
Les filtres seront alors appliqués indépendamment à chaque segment, cela nous permet d'utiliser les données du segment dans son ensemble pour choisir le filtre le plus approprié. Par exemple on peut se baser sur la densité spatiale des points (à savoir la distance moyenne entre deux points consécutifs) pour choisir le filtre. En effet les filtres mean filter et median filter ne sont efficaces que pour des trajectoires avec une bonne densité de points. On peut également utiliser cette information pour régler les paramètres du filtre : ici la taille de la fenêtre.
On teste donc ce filtrage par segment temporel avec les paramètres suivants :
- seuil de 400 secondes entre deux segments \n
- si la distance moyenne entre deux points sur un segment est inférieure à 20 mètres, on applique un median filter avec une fenêtre de taille 7
- si la distance moyenne entre deux points sur un segment est entre 20 et 50 mètres, on applique un median filter avec une fenêtre de taille 5
- si la distance moyenne entre deux points sur un segment est entre 50 et 150 mètres, on applique un mean filter avec une fenêtre de taille 5day_df3 = parser.selectDate("25-11-2017", android_df)
day_df3_filtered = filters.filterBySegment(day_df3, 400)
Comparaison aux données d'origine¶
gmap = gmplot.GoogleMapPlotter(45.757589, 4.831689, 14, apikey="AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM")
gmap.plot(day_df3["latitude"], day_df3["longitude"], "red", edge_width=5)
gmap.plot(day_df3_filtered["latitude"], day_df3_filtered["longitude"], "blue", edge_width=2)
gmap.draw("figure/4-segmented-filter-vs-original.html")
IFrame('figure/4-segmented-filter-vs-original.html', width=990, height=500)
Sur la carte ci-dessus on peut voir en bleu le trajet filtré et en rouge le trajet d'origine. On constate que, comme on s'y attendait, sur les trajets à grandes distances comme entre Lyon et Ecully le trajet filtré est fidèle au trajet d'origine (en effet les points sont assez éloignés pour qu'un point excentré par rapport aux autres puisse correspondre à un véritable détour plutôt qu'un outlier). En revanche sur les trajets où les points sont proches comme au niveau du domicile, le filtrage est plus fort et on exclue bien les points visiblement aberrants.
Cependant puisque la segmentation ne dépend que des délais, on peut se retrouver avec des situations où un segment comporte une partie peu dense et une partie dense, on aura alors une partie du segment qui ne sera pas traitée comme on l'espérait, comme c'est le cas ici au niveau de cenrale ou on est toujours sur le segment arrivant à centrale, et où on ne filtre donc pas bien les points pourtant proches.
Comparaison au median filter simple¶
On compare maintenant notre filtre par segment au median filter simple de fenêtre 5.
day_df3=filters.medianFilter(day_df3, 2)
gmap = gmplot.GoogleMapPlotter(45.757589, 4.831689, 14, apikey="AIzaSyDsYwvF3UUxTx8RB40wd4SnUVzfnbW66LM")
gmap.plot(day_df3["lat_med_filt"], day_df3["lng_med_filt"], "red", edge_width=5)
gmap.plot(day_df3_filtered["latitude"], day_df3_filtered["longitude"], "blue", edge_width=2)
gmap.draw("figure/4-segmented-filter-vs-median.html")
IFrame('figure/4-segmented-filter-vs-median.html', width=990, height=500)
On constate que globalement on gagne moins d'information qu'on n'en perd. En effet en quelques points on a bien une correction trop franche du median filter comme au niveau d'Anse où on perd le contournement du coude formé par la Saône. Mais on remarque qu'en contrepartie on garde encore un grand nombre d'outliers évidents.
Ce filtre nécessite donc un affinage, et si la segmentation temporelle reste pertinente pour détecter des arrêts d'utilisation du GPS, elle devrait intégrer une notion de découpage par densité de points.